Permutations

Philip J. Erdelsky

November 13, 2006

Please e-mail comments, corrections and additions to the webmaster at pje@efgh.com.

1. Introduction

A permutation of a set is a way of rearranging the elements of the set. For example, {1,2} and {2,1} are the two permutations of the set {1,2}.

The set {1,2,3} has six permutations: {1,2,3}, {1,3,2}, {2,1,3}, {2,3,1}, {3,1,2} and {3,2,1}.

A permutation may also be defined more formally as a one-to-one correspondence of a set with itself, a function which carries each element of the set into the one that occupies the same position after the permutation is applied. For example, the permutation {1,3,2} is the function f:{1,2,3} ⟶ {1,2,3} with f(1)=1, f(2)=3 and f(3)=2, or the set {(1,1), (2,3), (3,2)}. This way of thinking of permutations is especially useful if the elements of a set have no natural order.

Sometimes a permutation is illustrated by showing the set before and after the permutation, with an arrow from each element to its new position. For example, the permutations {1,3,2} and {2,1,3} can be illustrated as follows:

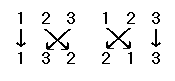
The identity permutation of a set is the permutation that leaves the set unchanged, or the function which maps each element to itself. In our example, the identity permutation is {1,2,3}.

2. Composition of Permutations

The composition of two permutations of the same set is just the composition of the associated functions. For example, the permutations {1,3,2} and {2,1,3} can be composed by tracing the destination of each element.

Start with
this element It is mapped by {1,3,2}
to this element which is mapped by {2,1,3}
to this element

1 1 2

2 3 3

3 2 1

Start with this element	It is mapped by {1,3,2} to this element	which is mapped by {2,1,3} to this element
1	1	2
2	3	3
3	2	1

Hence {1,3,2} ◌ {2,1,3} = {2,3,1}.

Similarly, it can be shown that {2,1,3} ◌ {1,3,2} = {3,1,2}

Start with
this element It is mapped by {2,1,3}
to this element which is mapped by {1,3,2}
to this element

1 2 3

2 1 1

3 3 2

Start with this element	It is mapped by {2,1,3} to this element	which is mapped by {1,3,2} to this element
1	2	3
2	1	1
3	3	2

This simple example shows that composition is not necessarily commutative (but it is associative).

The operations can be shown more clearly in graphic form:

If I is an identity permutation, and P is any permutation of the same set, then it is clear that I ◌ P = P ◌ I = P. There is also an inverse permutation P^-1 for which P^-1 ◌ P = P ◌ P^-1 = I. It can be found by taking the functional inverse, or by reversing each ordered pair in the definition of a function as a set of ordered pairs (and then sorting the ordered pairs by their new first elements).

For example, the inverse of {2,3,1} is the inverse of {(1,2), (2,3), (3,1)}, which is {(2,1), (3,2), (1,3)}, or {(1,3), (2,1), (3,2)}, or {3,1,2}.

Although composition of permutations is not commutative in general, it is commutative when one of the permutations or the result is the identity.

3. Even and Odd Permutations

Let p be a permutation of the set S = {1,2,3,...,n} (or any other totally ordered finite set). Consider a pair (i,j) of elements in S for which i<j. If p(i) > p(j) then the permutation is said to invert the order of (i,j).

The number of such pairs inverted by a permutation is not a very useful property of a permutation, but whether the number is even or odd turns out to be a useful property called the parity of the permutation. If the permutation inverts an even number of such pairs, it is said to be an even permutation; if it inverts an odd number of such pairs, it is said to be an odd permutation.

The identity permutation is obviously even; {2,1} is an example of an odd permutation.

Although it might appear that the definition of even and odd permutations depends on the ordering of the set, we shall prove that this is not the case.

An exchange is a permutation which interchanges two elements and leaves all other elements unmoved.

Lemma 3.1. Transposing two elements of a permutation of a finite set, which is equivalent to composing it with an exchange, changes an even permutation to an odd permutation, and vice-versa.

Proof. We first establish the lemma for two adjacent elements.

Let {p(1), p(2), ..., p(n)} be a permutation of {1,2,...,n}, and let k be an integer between 1 and n-1, inclusive. Then the permutation {p(1), p(2), ..., p(k+1), p(k), ..., p(n)} is the permutation with two adjacent elements p(k) and p(k+1) exchanged.

As we count inverted pairs in the new permutation, we see that all pairs that were inverted in the old permutation are also inverted in the new permutation, and vice-versa, except the pair (k, k+1), which changes from inverted to non-inverted, or vice-versa. Hence the number of inverted pairs in the new permutation is 1 more or less than the number in the old permutation. This establishes the lemma for adjacent pairs.

Now let i and j be two nonconsecutive integers between 1 and n, inclusive, where i < j, and consider the permutation in which p(i) and p(j) have been exchanged. We can accomplish this by a series of exchanges of consecutive elements. We move p(i) up to the j-th position by j-i exchanges of consecutive elements. First we exchange p(i) with p(i+1), then we exchange p(i) (which is now in the (i+1)-th position) with p(i+2), and so on until p(i) reaches the position formerly occupied by p(j). The following example, in which i=5 and j=9, should make this process clear:

     p(5), p(6), p(7), p(8), p(9)
     ----------
     exchange


     p(6), p(5), p(7), p(8), p(9)
           ----------
           exchange


     p(6), p(7), p(5), p(8), p(9)
                 ----------
                 exchange


     p(6), p(7), p(8), p(5), p(9)
                       ----------
                       exchange


     p(6), p(7), p(8), p(9), p(5)

Then we perform a similar sequence of j-i-1 exchanges in the opposite direction to move p(j) down to the position formerly occupied by p(i). In our example:

     p(6), p(7), p(8), p(9), p(5)
                 ----------
                 exchange

     p(6), p(7), p(9), p(8), p(5)
           ----------
           exchange

     p(6), p(9), p(7), p(8), p(5)
     ----------
     exchange

     p(9), p(6), p(7), p(8), p(5)

The result is the original permutation with p(i) and p(j) exchanged and other elements in their original positions. The number of exchanges of consecutive elements is (j-i) + (j-i-1), which is odd. Therefore the permutation has been changed from even to odd, or vice-versa. █

Notice that this lemma applies only if the exchange is applied after the permutation. However, it is clear that an exchange of i with j before a permutation p is equivalent to an exchange of p(i) and p(j) after the permutation. Hence the lemma applies in either case.

Theorem 3.2. Every permutation is a composition of exchanges, and is an even permutation if, and only if, the number of exchanges is even.

Proof. Let {p(1), p(2). ..., p(n)} be a permutation. Start with {1,2,...,n}. If p(1) is not 1, then a single exchange will bring it to the first position. If p(2) is not 2, then a single exchange will bring it to the second position. Proceding in this way, we can produce {p(1), p(2). ..., p(n)} as a composition of exchanges. The other part is a consequence of Lemma 3.1. █

Notice that this characterization of odd and even permutations does not depend on the order of the elements.

Corollary 3.3. The composition of two permutations of finite sets is even if, and only if, the two permutations are both even or both odd.

Corollary 3.4. A permutation of a finite set and its inverse are both even or both odd.

Theorem 3.5. A finite set with two or more elements has equal numbers of even and odd permutations.

Proof. For each even permutation, we can obtain a unique odd permutation by transposing the first two elements. This defines a one-to-one correspondence between even and odd permutations, hence there are equal numbers of each. █

A permutation may leave some elements of the set fixed. For example, {1,3,2,5,4} is an even permutation that leaves the element 1 fixed. If we consider only the effects on {2,3,4,5}, we have a permutation of a four-element set that is also even. The following theorem gives a more general result.

Theorem 3.6. If a permutation leaves one or more elements fixed, then the permutation restricted to other elements has the same parity as the original permutation.

Proof. The restricted permutation can be decomposed into restricted exchanges. These exchanges, when extended to the whole set, give the original permutation. Hence both permutations are even or odd. █

4. The Fifteen-Tile Puzzle

A popular puzzle involves a set of fifteen sliding tiles in a 4 ⨯ 4 square:

       1   2   3   4
       5   6   7   8
       9  10  11  12
      13  14  15

The sixteenth position is blank. The tiles can be rearranged by moving adjacent tiles into the blank. Through repeated moves of this kind, we can rearrange the tiles, as in this example:

       1   2   3   4      1   2   3   4      1   2   3   4
       5   6   7   8      5   6   7   8      5   6   7   8
       9  10  11  12      9  10  11  12      9  10      12
      13  15  14         13  15      14     13  15  11  14

       1   2   3   4      1   2   3   4
       5   6   7   8      5   6   7   8
       9  10  12          9  10  12  14
      13  15  11  14     13  15  11

Suppose we want to obtain the following result:

       1   2   3   4
       5   6   7   8
       9  10  11  12
      13  15  14

It is easy to show that this is impossible. Each arrangement is a permutation of sixteen items, where the blank space is considered as the sixteenth item. Each move involves the exchange of a tile with the blank space. The number of moves must be even, because the space must move up and down equal numbers of spaces, and right and left equal numbers of spaces, if it is to be returned to its original position in the lower right corner.

The desired result is an odd permutation, since it results from a single exchange. Hence it cannot be reached in the specified manner.