Elementary Set Theory Philip J. Erdelsky July 20, 2010

Please e-mail comments, corrections and additions to the webmaster at pje@efgh.com.

1. Introduction

Most, if not all, of pure mathematics is couched in the language of sets. You may notice that this section contains many definitions and only a few theorems. However, even a definition can contain a lot of mathematical wisdom. It took mathematicians centuries to formulate some fundamental definitions.

A set is a collection of items considered as a whole. If there are only a few items, the set can be defined by listing them in braces. For example, the set A might be defined as follows:

A = {1,2,3}

The items in a set are called elements or members of the set. They are also said to belong to the set or to be in the set, and the set is said to contain them. The symbol ∈ is used to express this relationship -- a∈ A means a belongs to A, and a∉ A means a does not belong to A.

Two sets are equal if they contain exactly the same elements. That is, set A is equal to set B if every element of A is also an element of B, and every element of B is also an element of A. The order in which the elements of a set are listed in its definition is irrelevant. For example, the sets {1,2,3} and {3,2,1} are equal.

An element cannot belong to a set more than once. Therefore, when a set is defined by listing its elements, each element is listed only once.

A set that contains no elements is called the empty set, and is represented by the symbol ∅.

If every element of the set A is also an element of the set B, then A is said to be a subset of B, represented symbolically by A⊆ B, or B is said to include A. Every set is a subset of itself, and the empty set is a subset of every set.

If A⊆ B and there is at least one element of B that is not an element of A, then A is said to be a proper subset of B, represented symbolically by A⊂ B.

A subset is often defined by some property of its elements. For example, let A = {1,2,3,4,5,6}, and let B = {2,4,6}. Then B could be defined as the set of all elements of A which are even, or in symbols:

B ={x∈ A | x is even}.

Here the symbol | means "such that". The word "all" is understood. In some cases the set A may also be understood.

The intersection of any number of sets is the set of elements that they all have in common. For example, the intersection of {1,2,3,4,5}, {2,3,4,5,6,7,8,9} and {3,5,7,9} is {3,5}. It is clear that the intersection of a collection of sets is a subset of every set in the collection. The intersection of two sets A and B is represented symbolically by A∩B.

The intersection operation has several obvious properties:

• Commutativity: A∩B = B∩A.
• Associativity: (A∩B)∩C = A∩(B∩C).
• A∩B = A if, and only if, A⊆ B.

The union of any number of sets is the set of all of their elements. For example the union of {1,2,3,4,5}, {2,3,4,5,6,7,8,9} and {3,5,7,9} is {1,2,3,4,5,6,7,8,9}. It is clear that every set in a union is a subset of their union. The union of two sets A and B is represented symbolically by A∪B.

The union operation has several obvious properties:

• Commutativity: A∪B = B∪A.
• Associativity: (A∪B)∪C = A∪(B∪C).
• A∪B = B if, and only if, A⊆ B.

Two sets are said to be disjoint if they have no elements in common; i.e., A and B are disjoint if A∩B = ∅. Three or more sets are said to be disjoint if every two of them are disjoint.

The notation A-B is used to indicate the set of all elements of A that are not elements of B. This operation has no standard name, but when B is a subset of A, A-B is sometimes said to be the complement of B in A.

The relationships among sets are often represented pictorially by a Venn diagram, in which sets are represented as the interiors of overlapping circles (or other plane figures). Set combinations are represented by areas bounded by the circles, as shown in the following example for two sets:

2. Ordered Pairs

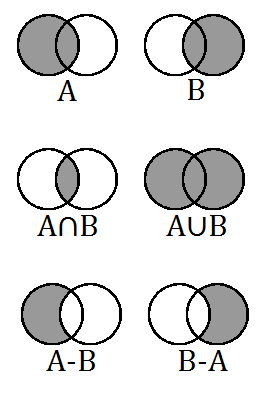
An ordered pair is a set of two elements in a specified order. An ordered pair is usually written (a,b) where a is the first element and b is the second element. Two ordered pairs (a,b) and (c,d) are equal if a=c and b=d. Reversing the elements of an ordered pair produces a different ordered pair if the elements are not the same. For example, the ordered pair (1,2) is not equal to the ordered pair (2,1).

For two sets A and B, the cross product A⨯ B is the set of all ordered pairs whose first and second elements are elements of A and B, respectively. That is,

A⨯ B = {(a,b) ∣ a∈ A and b∈ B}

Ordered triples, quadruples, etc. could be defined, but they are seldom needed.

3. Relations

A relation R on a set A is simply a set of ordered pairs of elements of A, i.e., R ⊆ A⨯ A. Two elements a and b are said to obey the relation if (a,b) is in R. However, for most relations, the set notation is not used. Instead, a symbol such as ~ placed between the elements to indicate that they obey the relation; for example a~b means that (a,b) is in R.

Other symbols often used for relations are

= > < ≥ ≤ ∣ ≠ ⊃ ⊂ ⊇ ⊆ ≡

Most useful relations have some additional properties. A relation ~ on the set A is an equivalence if the following hold for every a, b and c in A:

• It is reflexive: a~a.
• It is symmetric: a~b implies that b~a.
• It is transitive: a~b and b~c imply that a~c.

A set of nonempty subsets of a set A is called a partition of A if each element of A belongs to one and only one of the subsets; i.e., if the subsets are disjoint and their union is A. The following theorem establishes a connection between an equivalence relation and a partition.

Theorem 3.1. If ~ is an equivalence relation on the set A, then there is partition of the set A such that a~b if, and only if, a and b belong to the same set in the partition. Conversely, if P is a partition of A, then "a and b belong to the same set in P" is an equivalence relation.

Proof. Consider the set P of subsets T_a = {x ∈ A | x~a}. Clearly every a in A belongs to at least one subset in P, namely T_a. Hence the sets in P are nonempty and their union is A.

Now let T_a and T_b be two subsets in P. If they have an element c in common, then c~a, c~b and x~b for every x ∈ T_b. By transitivity x~a and x ∈ T_a, too. Similar arguments show that every element of T_a is also an element of T_b. Hence T_a and T_b are equal. If two subsets in P have no element in common, they are disjoint. Hence P is the desired partition.

The converse is trivial. █

The sets in the partition associated in this way with an equivalence relation are called its equivalence classes. They are often used to define mathematical systems.

Equivalence relations on two sets A and B can be used to define an equivalence relation on A⨯ B in the obvious way: (a,b) is equivalent to (c,d) if a is equivalent to c and b is equivalent to d.

4. Order

A partial order on a set A is a relation ≤ with the following properties for every a, b and c in A:

• It is reflexive: a ≤ a.
• It is antisymmetric: a ≤ b and b ≤ a imply that a = b.
• It is transitive: a ≤ b and b ≤ c imply that a ≤ c.

A partial order ≤ on the set A is called a linear order (or a total order) if, for every two elements a and b of A, a ≤ b or b ≤ a (or both, if a = b).

The set of all subsets of a set is partially ordered by inclusion: S ≤ T means S⊆ T. This partial order is usually not a total order because we can find two subsets, such as {1,2,3} and {2,3,4}, such that neither is a subset of the other.

The familiar relation ≤ in arithmetic is a total order.

In working with a partial or total order, it is common to define some associated relations:

• a ≥ b means b ≤ a,
• a < b means a ≤ b and a ≠ b,
• a > b means b ≤ a and b ≠ a.

There is an alternative way to define partial and total orders. A relation < is a partial order if obeys the following two conditions:

• It is transitive: a < b and b < c imply that a < c.
• a < a is always false.

A partial order is a total order if it is also trichotomous: for any two elements a and b, one and only one of the following holds:

• a < b,
• a = b,
• b < a.

The other relations are then defined in terms of <:

• a ≤ b means a < b or a = b.
• a ≥ b means b < a or a = b.
• a > b means b < a.

It can be shown that the two ways of defining partial and total orders are equivalent.

Generally, the names "partial order" and "total order" are applied to the entire set of relations ≤, <, > and ≥ without specifying which is the order relation and which are associated with it.

5. Functions

A function f from the set A to the set B is a rule which, given any element x of A, produces exactly one corresponding element of B represented by f(x). This concept is often expressed symbolically as f:A⟶B.

A function is also called a mapping. Both names are commonly used in mathematics, but from this point forth we will use the name function.

A second, and more abstract, way to define a function f:A⟶B is as subset of A ⨯ B such that for every element x of A there is one and only one ordered pair in the subset whose first element is x. The second element of the pair is then defined to be f(x).

The element f(x) is called the image of x under the function. The function f is also said to map or carry the element x to the element f(x).

If f:A⟶B then A is called the domain of f, and the set of all elements of B which are images of elements in A is called the range of f. The sets A and B need not be different; in fact, they are the same in many applications.

Some functions have special properties that make them especially interesting or useful. If f:A⟶B, then

If the range is equal to B, then f is called a surjection, a surjective function, or a function of A onto B. The function is sometimes also said to be "onto", but the use of a preposition as an adjective sounds so stilted that good writers tend to avoid it.

If the range is a proper subset of B, then f is called a function of A into B.

If the f carries at most one element of its domain into each element of its range, i.e., if f(x) = f(y) implies that x = y, then f is called an injection, an injective function, or a one-to-one function.

If f is both surjective and one-to-one then it is called a one-to-one correspondence of A and B. If f is one-to-one but not surjective, then it is a one-to-one correspondence of A and its range, which is a proper subset of B.

If f:A⟶B is a one-to-one correspondence then it has an inverse function called f ^-1:B⟶A defined by

f ^-1(x) = the element w of A such that f(w) = x.

Of course, the converse is also true. If a function has an inverse, then it is a one-to-one correspondence.

Two functions f:A⟶B and g:A⟶B are equal if f(x) = g(x) for every x in A.

If the range of one function is a subset of the domain of another, then a composite function is defined by applying the functions successively. That is, if f:A⟶B and g:B⟶C then the composite function (f◌g):A⟶C is defined by

(f ◌g)(x) = g(f(x)) for every x in A.

If the functions have appropriate domains and ranges, composition is associative, i.e, (f ◌g) ◌h = f ◌(g ◌h).

A one-to-one function f:A⟶B of two sets with some structure is called an isomorphism if it preserves the structure. We have seen one example of a set with structure: the partially ordered set. If the sets A and B are partially ordered, then f:A⟶B is an isomorphism if it is one-to-one, surjective, and f(x) < f(y) if, and only if, x < y.

An isomorphism of a structured set with itself is called an automorphism. Clearly, the identity function (f(x) = x for all x) is an automorphism of any structured set. A good example of a nontrivial automorphism is the function which carries a complex number into its conjugate (i.e,. f(x+iy) = x-iy for all real x and y). It is one-to-one, surjective, and preserves addition and multiplication of complex numbers.

Suppose f:A⟶B and there are equivalence relations on the sets A and B. Let P_A and P_B be the corresponding sets of equivalence classes of A and B, respectively. If f carries equivalent elements of A into equivalent elements of B, i.e., if a ~ b implies that f(a) ~ f(b), then there is a unique function g:P_A ⟶P_B defined in the following manner. Let S be an equivalence class in P_A. Select any element a from this equivalence class and define g(S) to be the equivalence class containing f(a). It is easily shown that this does not depend on the particular element chosen from P_A. Moreover, g inherits many of the properties of f; e.g., if f is surjective, so is g.

5. Operations

A unary operation on a set is a function whose domain is that set. What distinguishes a unary operation from an ordinary function is the notation used, and often its relationships with other functions or operations. For example, the function that carries any real number x to the number -x is a unary operation called negation. The range of the function is often the same set, but this is not required.

A binary operation is a function whose domain is the cross product of two sets (or the cross product of a set with itself). For example, addition and multiplication are two binary operations on the set R⨯ R, where R is the set of real numbers. The image of an ordered pair (x,y) is usually written as x+y for addition and xy for multiplication. Here x and y are called the operands. The former notation is usually used only for addition, or operations very much like addition. The latter notation is used for more general operations.

Unary and binary operations are very common in mathematics; operations with three or more operands are rare, except for extensions of binary operations as noted below. Binary operations on a single set are more common than binary operations on pairs of sets, but both are encountered frequently.

A binary operation is said to be associative if it can be used on three operands without regard to their grouping, i.e., if

(xy)z = x(yz)
(x + y) + z = x + (y + z)

If a binary operation is associative, we can write the result for three operands without parentheses, making it a well-defined operation with three operands:

xyz = (xy)z = x(yz)
x + y + z = (x + y) + z = x + (y + z)

Ordinary addition and multiplication are associative; so are many other binary operations. The composition of functions is an associative binary operation (provided the functions have suitable domains and ranges). In fact, most binary operations are associative.

If a binary operation is associative, it is easy to extend the property to operations on four or more operands:

wxyz = (wxy)z = (w(xy))z = w((xy)z) = w(xyz).

A binary operation is commutative if the order of the operands does not affect the result; i.e., if

xy = yx
x + y = y + x

If a commutative operation is also associative, commutativity can easily be extended to operations on three or more operands:

xyz = (xy)z = (yx)z = yxz = y(xz) = (yx)z = yxz, etc.

Binary operations which are commutative but not associative are very rare. Binary operations which are associative but not commutative are fairly common. Composition of functions is one example; a demonstration of that fact will be given later.

Now consider a binary operation on A⨯ B with its range in C (which need not be different sets). Suppose there are equivalence operations on these sets (which also need not be different), and the binary operation preserves equivalence, i.e., the operation when applied to equivalent operands gives equivalent results, or a ~ b and c ~ d imply that ac ~ bd. Then, just as a function of one variable was extended to a function on equivalence classes, an operation on two variables can be extended similarly. If a and b are any elements of the equivalence classes P and Q, respectively, then PQ is defined to be the equivalence class containing ab. The new operation inherits many properties of the old one, including associativity and commutativity.

Links

• Bulgarian translation by Stoil Dragomirov.
• Indonesian translation by Chameleon John.
• German translation by Daniel Gruber of akkuschraubercheck.de.