
|
Vector SpacesPhilip J. ErdelskyMay 15, 2015 |
Please e-mail comments, corrections and additions to the webmaster at pje@efgh.com.

|
Vector SpacesPhilip J. ErdelskyMay 15, 2015 |
Please e-mail comments, corrections and additions to the webmaster at pje@efgh.com.
Let F be a field and n a positive integer. An n-dimensional vector over F is a an ordered n-tuple x = (x1, x2, ..., xn) of elements of F, which are often called the components of x. An element of F is called a scalar. Two vectors are equal if they have the same dimension and their corresponding components are equal. Vectors are conventionally represented by boldface small letters.
We define addition of two vectors x and y as follows:
x = (x1, x2, ..., xn),
y = (y1, y2, ..., yn),
x + y = (x1 + y1, x2 + y2, ..., xn + yn).
It is easy to show that the set of all n-dimensional vectors is a commutative group under addition. The identity element is the zero vector O = (0, 0, ..., 0), and the inverse of x = (x1, x2, ..., xn) is -x = (-x1, -x2, ..., -xn).
We also define the multiplication of a vector by a scalar c:
x = (x1, x2, ..., xn),
cx = (cx1, cx2, ..., cxn).
It is easy to show that for any scalars c and d and any vectors x and y,
The set of all n-dimensional vectors, with these operations, is also called the n-dimensional coordinate space over the field F, represented by F n.
A linear combination of the vectors v1, v2, ..., vm is a sum of the following form:
c1 v1 + c2 v2 + ... + cm vm,where c1, c2, ..., cm are scalars called the coefficients of the linear combination.
The vectors v1, v2,..., vm are said to be linearly dependent (or simply dependent) if there is a nontrivial linear combination which equals the zero vector, i.e., if
c1 v1 + c2 v2 + ... + cm vm = O,where not all of the coefficients are zero. In this case, at least one of the vectors (one with a nonzero coefficient) is equal to a linear combination of the others. For example, if c1 ≠ 0, then
v1 = (-c2/c1) v2 + (-c3/c1) v3 + ... + (-cm/c1) vm.
The converse is also true. If one vector can be expressed as a linear combination of the others, the vectors are linearly dependent.
It is clear that any set of vectors containing the zero vector is linearly dependent, and that a linearly dependent set remains linearly dependent when additional vectors are appended to it.
Vectors which are not linearly independent are said to be linearly independent (or simply independent).
The following n n-dimensional vectors are linearly independent:
e1 = (1, 0, 0, ..., 0)
e2 = (0, 1, 0, ..., 0)
e3 = (0, 0, 1, ..., 0)
***
en = (0, 0, 0, ..., 1)
However, this is the maximum number of linearly independent n-dimensional vectors, as the following theorem shows.
Theorem 1.1. Any set of n+1 or more n-dimensional vectors over the same field are linearly dependent.
Proof. It is sufficient to prove that any set of n+1 n-dimensional vectors over the same field are linearly dependent. The proof is by induction on n.
For n = 1, the result is fairly obvious. If two vectors are both zero vectors, they are linearly dependent. If (a) and (b) are not both zero vectors, then the linear combination b(a) - a(b) = (0) shows them to be linearly dependent.
Now assume n > 1 and let v1, v2,..., vn, vn+1, be any set of n+1 n-dimensional vectors over the same field.
Let w1, w2,..., wn, wn+1 be the (n-1)-dimensional vectors obtained by eliminating the last components. By inductive hypothesis, w1, w2,..., wn are linearly dependent, so
c1 w1 + c2 w2 + ... + cn wn = (0, 0, ..., 0),
where the coefficients are not all zero. Assume the vectors have been arranged so c1 ≠ 0.
Similarly,
d2 w2 + d3 w3 + ... + dn+1 wn+1 = (0, 0, ..., 0),
where the coefficients are not all zero.
Now consider the corresponding linear combinations of the full vectors:
c1 v1 + c2 v2 + ... + cn vn = (0, 0, ..., 0, e),
d2 v2 + d3 v3 + ... + dn+1 vn+1 = (0, 0, ..., 0, f),
If e = 0 or f = 0 then one of these shows the n+1 vectors to be dependent. In other cases, we multiply the first equation by -f/e and add it to the second to obtain
(-(f/e)c1) v1 + (d2-(f/e)c2) v2 + ... + (dn-(f/e)cn) vn + dn+1 vn+1 = (0, 0, ..., 0, 0),
which shows the n+1 vectors to be linearly dependent, because the first coefficient, at least, is nonzero. █
Lemma 1.2. If the vectors v1, v2,..., vm are linearly independent, but the v1, v2,..., vm, vm+1 are linearly dependent, the additional vector vm+1 is a linear combination of v1, v2,..., vm.
Proof. By hypothesis,
b1 v1 + b2 v2 + ... + bm vm + bm+1 w = O,
where not all of the coefficients are zero. If bm+1 were zero, this would reduce to a nontrivial linear combination of v1, v2,..., vm which is equal to zero. This is impossible because v1, v2,..., vm are linearly independent. Hence bm+1 is nonzero, and the equation can be solved for w:
w = (-b1/bm+1) v1 + (-b2/bm+1) v2 + ... + (-bm/bm+1) vm,
which is the desired result. █
Theorem 1.3. Any set of fewer than n linearly independent n-dimensional vectors is non-maximal; i.e., another n-dimensional vector can be appended and the set will still be linearly independent.
Proof. Assume, for purpose of contradiction, that m < n and v1, v2,..., vm are a maximal set of linearly independent n-dimensional vectors.
By Lemma 1.2 every n-dimensional vector must be a linear combination of these vectors. In particular,
c1,1 v1 + c1,2 v2 + ... + c1,m vm = (1, 0, 0, ..., 0) (1.3.1)
c2,1 v1 + c2,2 v2 + ... + c2,m vm = (0, 1, 0, ..., 0)
***
cn,1 v1 + cn,2 v2 + ... + cn,m vm = (0, 0, 0, ..., 1)
Now let the coefficients in each row be an m-dimensional vector:
(c1,1, c1,2, ... c1,m)
(c2,1, c2,2, ... c2,m)
***
(cn,1, cn,2, ... cn,m)
By Theorem 1.1 these vectors are linearly dependent, so there are coefficients d1, d2,..., dn, not all zero, such that
d1(c1,1, c1,2, ... c1,m) + (1.3.2)
d2(c2,1, c2,2, ... c2,m) +
... +
dn(cn,1, cn,2, ... cn,m) = (0, 0, ..., 0)
Now multiply the i-th equation in (1.3.1) by di, add the resulting equations, and apply (1.3.2) to obtain:
(0, 0, ..., 0) = (d1, d2,..., dn),
which is impossible because not all of the components of the right member are zero. █
The n-dimensional vectors defined in Section 1 (sometimes called coordinate vectors) are an example of a more general structure called a vector space over a field. To qualify, a set of vectors must be a commutative group under vector addition, and scalar multiplication must obey the first four conditions given in Section 1:
The other two can be derived from these.
Linearly independent and linearly dependent vectors are defined in the same manner and the same results apply. The dimension dim(V) of a general vector space V is the maximum number of linearly independent vectors. A general vector space need not have a dimension. For example, the set of all sequences (x1, x2, x3, ...), with the obvious definitions of addition and scalar multiplication, has the following infinite set of vectors, of which every finite subset, no matter how large, is linearly independent:
(1, 0, 0, 0, ...)
(0, 1, 0, 0, ...)
(0, 0, 1, 0, ...)
(0, 0, 0, 1, ...)
etc.
Another vector space that has no dimension is the set of all continuous real-valued functions, in which addition and scalar multiplication of functions are defined in the usual manner: (f+g)(x) = f(x) + g(x), (cf)(x) = c f(x).
Vector spaces that have dimensions are said to be finite-dimensional and those that do not have dimensions are infinite-dimensional.
The n-dimensional vectors defined in Section 1 form an n-dimensional vector space under this definition. A set of n linearly independent vectors has been exhibited, and Theorem 1.1 shows that there are no sets of more than n linearly independent vectors.
The zero-dimensional vector space, which consists of a single zero vector, is not included in Section 1, but it is needed to avoid inelegant exceptions to some results.
A basis for a vector space is a finite set of vectors such that every vector in the space can be expressed uniquely as a linear combination of the vectors in the basis. For example, the following n-dimensional vectors are a basis, which is usually called the canonical basis:
e1 = (1, 0, 0, ..., 0)
e2 = (0, 1, 0, ..., 0)
e3 = (0, 0, 1, ..., 0)
***
en = (0, 0, 0, ..., 1)
If a vector space does have a dimension n, then every set of n linearly independent vectors is a basis. Moreover, the basis v1, v2,..., vn establishes an isormophism between the vector space and the n-dimensional vectors over the same field:
c1 v1 + c2 v2 + ... + cn vn <-> (c1, c2, ..., cn)
This provides a somewhat more elegant statement of the proof of Theorem 1.3. If the m vectors were maximal, they would provide an isomorphism between vectors spaces of different dimensions.
These results can be summarized in a formal theorem:
Theorem 2.2. In a vector space of positive finite dimension n, every set of n linearly independent vectors is a basis, every set of fewer than n linearly independent vectors is a proper subset of a basis, and every basis contains n linearly independent vectors.
A subspace of a vector space is a subset that is a vector space over the same field with the same operations. Hence if x and y are any elements of the subset, and c is any scalar, x + y and cx are in the subset. A proper subspace is a subspace that is a proper subset. A subspace consisting of only the zero vector is called a trivial subspace; other subspaces are nontrivial.
Some properties of subspaces are fairly obvious:
Given a set S of vectors in a vector space (which may or may not have a dimension), the set of all linear combinations of the vectors in S constitutes a subspace, called the linear span of S, or the subspace spanned by S.
Theorem 2.3 If a subset S of a vector space has a maximum number n of linearly independent vectors, then its linear span has dimension n.
Proof. Any vector in S can be expressed as a linear combination of n linearly independent vectors in S. Clearly a linear combination of vectors in S can, by combining like terms, be expressed as a linear combination of the same n vectors. Since the vectors are linearly independent, the representation is unique. Hence the linear span is isomorphic to the space of n-dimensional vectors defined in Section 1, and its dimension is n. █
Theorem 2.4 If two subspaces S and T have dimensions, then the dimension of the subspace spanned by their union is dim(S) + dim(T) - dim(S ∩ T).
Proof. Start with a basis for S ∩ T and extend it to bases for S and T. The union of the two extended bases has the required number of vectors, and their linear span is the subspace spanned by S ∪ T. We must show that they are linearly independent. Take a linear combination of the vectors in the union that adds up to zero and write it as O = x + s + t, where x is a linear combination of vectors in the basis for S ∩ T, s is a linear combination of the additional vectors in the basis for S, and t is a linear combination of the additional vectors in the basis for T. Then clearly s ∈ S, t ∈ T, x ∈ S and x ∈ T. Also, s = -x-t, so s ∈ T also. Hence s ∈ S ∩ T, but since it is a linear combination of additional vectors independent of those in the basis for S ∩ T, s = O, and this is possible only if all coefficients in its definition are zero. Similarly, all coefficients in the definition of t are zero. This leaves x = O, which proves that the linear combination is trivial. █
Corollary 2.5 If two subspaces S and T of V have dim(S) + dim(T) > dim(V), then S and T have a nonzero vector in common.
The zero-dimensional vector space is not necessarily an exception; most of the definitions can be stretched to accommodate it. Its basis is empty, and an empty linear combination always evaluates to the zero vector.
The direct sum of two vector spaces R and S over the same field is the set of ordered pairs R ⨯ S, where addition and scalar multiplication are defined as follows:
(r1,s1) + (r2,s2) = (r1+r2,s1+s2),
c (r1,s1) = (cr1,cs1)
The direct sum is usually written as R ⊕ S. It is easily shown that the direct sum is an associative and commutative operation, in the sense that R ⊕ S is isomorphic to S ⊕ R and (R ⊕ S) ⊕ T is isomorphic to R ⊕ (S ⊕ T), and that dim(R ⊕ S) = dim(R) + dim(S)).
Although any two distinct vector spaces over the same field have a direct sum, two subspaces of the same space have a direct sum only if they have only the zero vector in common. In this case R ⊕ S is the subspace consisting of all vectors of the form r+s where r ∈ R and s ∈ S. It is easily shown that direct sums formed in this way are isomorphic to those formed from distinct vector spaces.
Since the direct sum is associative, direct sums of three or more spaces can be built up from direct sums of two spaces; e.g., R ⊕ S ⊕ T = (R ⊕ S) ⊕ T = R ⊕ (S ⊕ T).
Equivalently, the direct sum V = S1 ⊕ S2 ⊕ ... ⊕ Sm of three or more subspaces can be defined directly if every element of V can be expressed uniquely as a sum s1 + s2 + ... + sm, where sk ∈ Sk. It is easily shown that any union of bases for the subspaces is a basis for V. It can also be shown that if the subspaces S1, S2, ..., Sm have disjoint bases whose union is a basis for V, then V is their direct sum.
Direct sums are actually a generalization of the concept of bases. Subspaces S1, S2, ..., Sm, all of nonzero dimension, are linearly dependent if there is a set of m vectors, one from each subspace, whose sum is zero even though not all of the vectors in the sum are zero. A set of linearly independent subspaces constitutes a generalized basis for their linear span, in the sense that any vector in the linear span can be expressed uniquely as a sum of vectors, one from each subspace. The dimension of the linear span of linearly independent subspaces is the sum of their dimensions.
Observations of this kind, which are fairly easy to prove, are often referred to as "dimensionality arguments" without elaboration.
One-dimensional, two-dimensional and three-dimensional vectors over the field of real numbers have a geometric interpretation. Reasoning by analogy, we can extend many geometric properties to four or more dimensions.
The one-dimensional vector (x) is associated with a point on a straight line x units to the right of the origin if x ≥ 0, or -x units to the left if x < 0.
The two-dimensional vector (x1, x2) is associated with the point in two-dimensional coordinate system whose abscissa and ordinate are x1 and x2, respectively.
Similarly, the three-dimensional vector (x1, x2, x3) is associated with the point in a three-dimensional coordinate system whose coordinates are x1, x2 and x3.
Spaces with four or more dimensions are defined in the same way. In some applications, a vector is thought of, not as a point, but as a line running from the origin to the point.
Let S be a subspace of a vector space and let p be a point in the space (but not necessarily in the subspace). The set p + S, which consists of all sums of the form p + s where s is any element of S, is a hyperplane of dimension dim(S). Hyperplanes of dimensions 0, 1 and 2 are called points, lines and planes, respectively.
Another way to define a hyperplane p + S is to say that it contains all vectors x such that x - p ∈ S.
A hyperplane that passes through the origin is a subspace of the same dimension.
The subspace S in the representation of a hyperplane p + S is unique, but p is not. Any point on the hyperplane will do.
Using dimensionality arguments, we can prove some familiar properties of points, lines and planes and extend them to higher dimensions.
A useful technique in geometry is translation, a one-to-one mapping of the form f(x) = x + t for some constant vector t. It is easy to see that translation carries hyperplanes into hyperplanes of the same dimension.
It is well known that two distinct points determine a line, and that three points that do not lie on the same straight line determine a plane.
In general, m+1 points that do not lie on the same (m-1)-dimensional hyperplane determine a unique m-dimensional hyperplane. To prove this, we first translate the points so one of them lies at the origin. This reduces the problem to a simple property of subspaces: m points that do not lie in the same (m-1)-dimensional subspace (i.e., that are linearly independent) determine a unique m-dimensional subspace.
Of special interest are (n-1)-dimensional hyperplanes in n-dimensional space (lines in two-dimensional space, planes in three-dimensional space, etc.). Two such hyperplanes are (1) identical, (2) parallel (disjoint), or (3) their intersection is an (n-2)-dimensional hyperplane.
To prove this, let p+S and q+T be the two hyperplanes. In the case where S = T, if the two hyperplanes have any point in common, they are identical. This covers cases (1) and (2). If S ≠ T, then a dimensionality argument based on Theorem 2.4 shows that dim(S ∩ T) = n-1 and their union spans the entire n-dimensional space. Hence there are elements s and t of S and T, respectively, such that s+t = p-q. Therefore p-s = q+t and the two hyperplanes have a point in common. The intersection of the two hyperplanes is p-s+(S ∩ T), which is an (n-2)-dimensional hyperplane.
If x and y are two linearly independent vectors, then O, x, y and x+y lie at the vertices of a parallelogram. This is fairly easy to prove. First of all, the points lie in a plane; the two points x and y determine the plane, and O and x+y lie in it. Let X be the one-dimensional subspace spanned by x. Then the line determined by O and x is O + X, and the line determined by y and x+y is y + X. They are obviously parallel. Similarly, the other two sides are parallel.
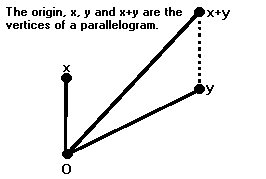
If x and y are two n-dimensional vectors over the field of real numbers, the inner product x ∙ y is the scalar defined by
x = (x1, x2, ..., xn),
y = (y1, y2, ..., yn),
x ∙ y = x1 y1 + x2 y2 + ... + xn yn.
An alternate notation for the inner product is (x, y).
The following properties of the inner product are easily verified, where x, y and z are any vectors and c is any scalar:
Any operation on a vector space over the field of real numbers that has these properties is called an inner product. The one defined for n-dimensional vectors is not the only possible inner product. (For example, 2(x ∙ y) is another possibility.) Later, we will prove that such a space, which is usually called an inner-product space, is isomorphic to the n-dimensional vectors and the inner product defined here.
The norm (or length) of a vector x is represented by ∥x∥ and defined to be the principal (nonnegative) square root of x ∙ x. If the dimension is no more than three, this is the usual distance from the origin to the point represented by the vector, according to the Pythagorean Theorem. The distance between points x and y is ∥x-y∥. We extend it by analogy to higher dimensions.
Some important properties of the norm are as follows, where x is any vector and c is any scalar:
Any function on a vector space over the field of real numbers that has these properties is called a norm, although we shall use only the one derived from the inner product. Because it conforms to the notion of distance in Euclidean geometry, it is often called the Euclidean norm.
The first two properties are fairly obvious; it is the third one that requires a detailed proof. The following theorem is called the Cauchy-Schwarz Inequality (or the Cauchy-Bunyakovski-Schwarz Inequality, or the CBS Inequality). It is a fundamental theorem in a number of branches of mathematics.
Theorem 4.1 For any two vectors x and y, ∣x ∙ y∣ ≤ ∥x∥ ∥y∥, with equality only when x and y are linearly dependent.
Proof. The assertion is obvious if x and y are linearly dependent. If they are linearly independent, consider the linear combination (x ∙ x) y - (x ∙ y) x. It must be nonzero, because the first coefficient, at least, is nonzero. Hence its inner product with itself must be positive:
[(x ∙ x) y - (x ∙ y) x] ∙ [(x ∙ x) y - (x ∙ y) x] > 0.
We use the properties of inner products to multiply out the left member:
(x ∙ x)2(y ∙ y) - 2 (x ∙ x)(x ∙ y)2 + (x ∙ y)2(x ∙ x) > 0.
We combine like terms:
(x ∙ x)2(y ∙ y) - (x ∙ x)(x ∙ y)2 > 0.
We divide both terms by (x ∙ x):
(x ∙ x)(y ∙ y) - (x ∙ y)2 > 0,
We move the second term to the right side:
(x ∙ x)(y ∙ y) > (x ∙ y)2.Taking the principal square root of each side produces the desired result. █
We are now ready to establish the third property of norms, starting with the Cauchy-Schwarz inequality for linearly independent vectors:
∣x ∙ y∣ < ∥x∥ ∥y∥.
Since x ∙ y ≤ ∣x ∙ y∣, this implies that
x ∙ y < ∥x∥ ∥y∥.
Multiply by 2 and add some extra terms:
x ∙ x + 2 (x ∙ y) + y ∙ y < x ∙ x + 2 ∥x∥ ∥y∥ + y ∙ y.
Factor each member:
(x + y) ∙ (x + y) < (∥x∥ + ∥y∥) 2.
Then take the principal square root of each side to obtain the desired result:
∥x + y∥ < ∥x∥ + ∥y∥.
The result for linearly dependent vectors is easy to prove.
This result is often called the triangle inequality. If the vectors x, y and x + y are arranged in a triangle, the inequality states that the distance from one vertex to another, when measured along the side joining them, is less than the distance measured along the other two sides. It is a special case of the general principle that the shortest distance between two points is a straight line.
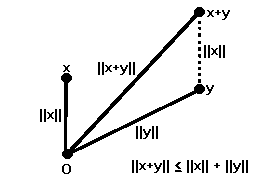
Two vectors x and y are said to be perpendicular or orthogonal if x ∙ y = 0. This is a matter of definition, but it conforms in one respect to the usual definition of perpendicular. If x and y are perpendicular, then the angle made by x and y is equal to the angle made by -x and y.
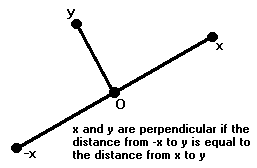
We don't have a definition of angles yet, but this will surely be the case if the distance from -x to y is equal to the distance from x to y:
∥-x-y∥ = ∥x-y∥.
We can square each side to obtain an equivalent equation:
∥-x-y∥ 2 = ∥x-y∥ 2.
Using the definition of the norm and the properties of inner products, we can perform some obvious algebraic manipulations:
(-x-y) ∙ (-x-y) = (x-y) ∙ (x-y),
x ∙ x + 2(x ∙ y) + y ∙ y = x ∙ x - 2(x ∙ y) + y ∙ y,
2(x ∙ y) = -2(x ∙ y),
which holds if and only if x ∙ y = 0.
A set of vectors v1, v2, ..., vn in a vector space over the field of real numbers is called orthogonal if every pair of vectors is orthogonal; i.e., vi ∙ vj = 0 if i ≠ j.
The canonical basis vectors are an orthogonal set:
e1 = (1, 0, 0, ..., 0)
e2 = (0, 1, 0, ..., 0)
e3 = (0, 0, 1, ..., 0)
***
en = (0, 0, 0, ..., 1)
It is easy to show that nonzero orthogonal vectors are linearly independent. Suppose that
c1v1 + c2v2 + ... + cnvn = 0.
Take the inner product of both sides with vi:
vi ∙ (c1v1 + c2v2 + ... + cnvn) = 0.
Then apply the properties of inner products to obtain:
c1 vi ∙ v1 + c2 vi ∙ v2 + ... + ci vi ∙ vi + ... + cn vi ∙ vn = 0
Because the vectors are orthogonal, all terms but one vanish:
ci (vi ∙ vi) = 0.
Since vi is nonzero, this implies that ci = 0.
Hence nonzero orthogonal vectors constitute a special kind of basis for their linear span, which is called an orthogonal basis.
Every basis can be converted to an orthogonal basis for the same subspace by a procedure called the Gram-Schmidt Process. We describe this process by induction on the number n of vectors.
For n=1, the process is vacuous; a single nonzero vector is an othogonal set.
For higher values of n, use the process with n-1 vectors to create an orthogonal basis w1, w2, ..., wn-1 for the linear span of the first n-1 vectors in the original set.
Let vn be the n-th vector in the original set and replace it by
wn = vn - [(vn ∙ w1)/(w1 ∙ w1)] w1 - [(vn ∙ w2)/(w2 ∙ w2)] w2 - ... - [(vn ∙ wn-1)/(wn-1 ∙ wn-1)] wn-1.
Then it is easily shown that w1, w2, ..., wn is the desired orthogonal basis.
An orthogonal basis in which every basis vector is of unit length (such as the canonical basis noted above) is called an orthonormal basis. Any orthogonal basis can be converted to an orthonormal basis by replacing each vector v by the vector v/∥v∥. This is called normalizing the vector.
Orthonormal bases are especially useful because it is easy to express any vector in terms of the basis. For example, suppose that
x = c1 w1 + c2 w2 + ... + cn wn.
Take the inner product of each side with wk to obtain
wk ∙ x = c1(wk ∙ w1) + c2(wk ∙ w2) + ... + ck(wk ∙ wk) + ... + cn(wk ∙ wn).
With the orthonormality properties, this reduces to
wk ∙ x = ck.
Therefore,
x = (w1 ∙ x) w1 + (w2 ∙ x) w2 + ... + (wn ∙ x) wn.
Moreover, the inner product of two vectors expressed in terms of an othonormal basis is
(c1 w1 + c2 w2 + ... + cn wn) ∙ (d1 w1 + d2 w2 + ... + dn wn) = c1 d1 + c2 d2 + ... + cn dn.because wi ∙ wj is 1 if i = j and 0 otherwise. This is the way the inner product was defined for n-dimensional vectors.
If S is a subspace of an n-dimensional vector space, then the orthogonal complement S ⊥ is the set of all vectors that are orthogonal to every vector in S. The following properties of orthogonal complements are fairly easy to prove:
Inner products and norms can be defined over more general real vector spaces. For example, consider the set of all continuous real-valued functions over some closed interval [a,b], in which addition and scalar multiplication of functions are defined in the usual manner: (f+g)(x) = f(x) + g(x), (cf)(x) = c f(x). The inner product can be defined as
f ∙ g = ∫ab f(x) g(x) dx.
If a = 0 and b = 2π, then the functions sin(x), sin(2x), sin(3x) ... and 1, cos(x), cos(2x), cos(3x) ... are orthogonal.
Inner products are usually defined over real vector spaces, but they can also be defined over complex vector spaces, with some modifications. If u and v are two n-dimensional vectors over the field of complex numbers, the complex inner product u ∙ v is the scalar defined by
u = (u1, u2, ..., un),
v = (v1, v2, ..., vn),
u ∙ v = ū1 v1 + ū2 v2 + ... + ūn vn.
The following properties of the complex inner product are easily verified, where x, y and z are any vectors and e is any scalar:
We wish to define an angle between two lines in a way that is consistent with Euclidean geometry in two and three dimensions. Consider the angle A formed by the point x, the origin and the point y.
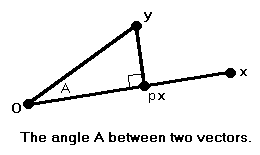
We first drop a perpendicular from y to the line joining the origin to x. Clearly, the base of the perpendicular is a scalar product px, which we can compute as follows:
x ∙ (y - px) = 0,
x ∙ y - px ∙ x = 0,
p = (x ∙ y) / (x ∙ x).
If the angle is acute p > 0, and it is given by
cos(A) = ∥px∥ / ∥y∥ = p ∥x∥ / ∥y∥ = [(x ∙ y) / (x ∙ x)] (∥x∥ / ∥y∥), cos(A) = (x ∙ y) / (∥x∥ ∥y∥).
It can be shown that this formula also applies if the angle is a right
angle or an obtuse angle.
Links