|
A Piece of πPhilip J. ErdelskyJuly 26, 2001 |
Please e-mail comments, corrections and additions to the webmaster at pje@efgh.com.
|
A Piece of πPhilip J. ErdelskyJuly 26, 2001 |
Please e-mail comments, corrections and additions to the webmaster at pje@efgh.com.
Mathematics contains many interesting transcendental constants, but only one of them was known to the ancients. It is π, the ratio of the circumference to the diameter of a circle.
Archimedes was the first mathematician to compute an approximate value for π. Previous values had been based on physical measurements of limited accuracy.
We will use Archimedes' method to compute an approximate value of π, using only mathematics known to Archimedes. However, we will be doing our computations on a computer, and we will get a much more accurate value than he did.
The ancients didn't have a very good theory of limits; neither do most non-mathematicians. But some things are fairly obvious. A regular polygon with many sides is approximately a circle. Its perimeter is approximately the circumference of the circle, and its area is approximately the area of the circle. The more sides the polygon has, the more accurate the approximation. If the polygon has enough sides, any desired degree of accuracy can be obtained.
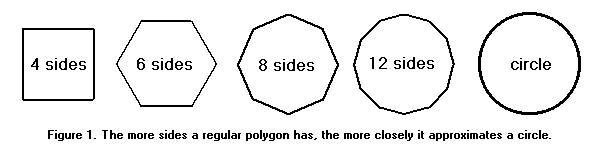
To find an approximate value for π, we will inscribe regular polygons in a circle of radius 1. The perimeters of the polygons can be computed in some cases, using nothing more advanced than the Pythagorean theorem, which was known to Archimedes. In particular, if we know the length of each side of the regular polygon with n sides, we can compute the length of each side of the regular polygon with 2n sides.
In Figure 2, let AB be one of the n sides of a regular polygon inscribed in a circle with center at O and a radius one unit long. Let s be the length of AB.
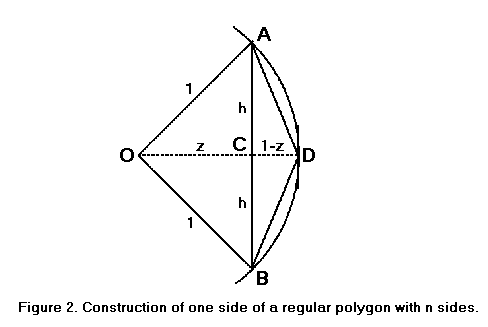
Let OCD be the bisector of the angle AOB. Then triangles AOC and BOC are congruent; hence the angles at C are right angles and AC = CB. Therefore,
The perimeter of the polygon is ns and the diameter of the circle is 2. Hence the approximate value of π is ns/2.
The line segments AD and BD are sides of an inscribed polygon with 2n sides. The length of each one is
In the case where n = 6, we know that s = 1. This is a well-known fact, but we shall give a short proof. Because the hexagon is regular, all six angles at the center are equal. The angle ACB is inscribed in a circle, so it is half the intercepted angle AOB, which is equal to two of the six angles. Hence angle ACB is equal to angle BOC. The opposite sides OB and BC are also equal. Similar arguments show every other side to be as long as the radius of the circle.
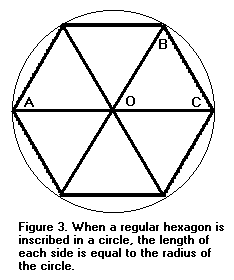
All we have to do is apply this formula repeatedly to get values for n = 12, 24, 48, 96, etc.
A simple computer program, like the following C++ program, will perform these computations quickly.
#include <stdio.h>
#include <math.h>
void main(void)
{
double s = 1.0;
double n = 6.0;
puts("number of sides approximate value of pi");
while (n < 500000000.0)
{
printf ("%9.0f %18.16f\n", n, n*s/2.0);
double h = s / 2.0;
double z = sqrt(1.0 - h * h);
s = sqrt(h * h + (1.0 - z) * (1.0 - z));
n *= 2;
}
}
The results look like this:
number of sides approximate value of pi
6 3.0000000000000000
12 3.1058285412302489
24 3.1326286132812378
48 3.1393502030468667
96 3.1410319508905098
192 3.1414524722854624
384 3.1415576079118579
768 3.1415838921483186
1536 3.1415904632280505
3072 3.1415921059992717
6144 3.1415925166921577
12288 3.1415926193653840
24576 3.1415926450336911
49152 3.1415926514507682
98304 3.1415926530550373
196608 3.1415926534561045
393216 3.1415926535563719
786432 3.1415926535814380
1572864 3.1415926535877046
3145728 3.1415926535892713
6291456 3.1415926535896630
12582912 3.1415926535897611
25165824 3.1415926535897856
50331648 3.1415926535897913
100663296 3.1415926535897931
201326592 3.1415926535897931
402653184 3.1415926535897931
Archimedes, with nothing better than an abacus to compute with, had to stop at 96 sides.
A Portuguese translation of this article by Artur Weber & Adelina Domingos is available at www.homeyou.com/~edu/um-pedaco-de-pi.
A Turkish translation of this article is available at thesciencexperts.com/bir-parca-%CF%80.